Often in the physical sciences one is asked to fit the best line to a set of experimental data points. This is called linear regression. Most plotting programs include this linear regression capability, but often it is more beneficial to plot the experimental data on graph paper for the determination of unknown quantities. For that reason, it is useful to have the equations available that lets one mathematically fit the best line to a set of experimental observations.
The equations for linear regression can be derived from the Calculus
of minimization. We will skip this derivation and proceed straight to
the equations. Remember that the equation for a line is y=mx+b. The
coefficents m and b can be solved for explicitly by solving a
set of simultaneous equations.
| |
(1) |
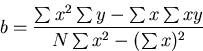 |
(2) |
Assume one has the following data from the Ni2+ spectrophotometry experiment.
| Solution # | Concentration | % T | Absorbance |
| 1 | 0.1526 | 75.0 | 0.1250 |
| 2 | 0.0610 | 83.0 | 0.0809 |
| 3 | 0.0305 | 89.5 | 0.0482 |
| 4 | 0.0153 | 95.3 | 0.0209 |
| 5 | 0.0061 | 97.7 | 0.0101 |
| Symmation | Value |
| N | 5 |
| 0.2655 | |
| 0.2851 | |
| 0.02821 | |
| 0.02586 |
| y = 0.7599 x + 0.01167 | (3) |
This document was generated using the LaTeX2HTML translator Version 97.1 (release) (July 13th, 1997)
Copyright © 1993, 1994, 1995, 1996, 1997, Nikos Drakos, Computer Based Learning Unit, University of Leeds.
The command line arguments were:
latex2html -split 0 -local_icons regress.tex.
The translation was initiated by Andrew Pounds on 2/29/2000