Andrew J. Pounds, Ph.D.
Department of Chemistry, Mercer University
When one considers the normal distribution curve, one can claim that
68.3% of all the values fall between
![]() where
where ![]() is the population standard deviation based on a large number
(theoretically infinite) number of trials. This interval is known
as a confidence interval and its limits as confidence limits.
is the population standard deviation based on a large number
(theoretically infinite) number of trials. This interval is known
as a confidence interval and its limits as confidence limits.
When only a limited number of measurements of a quantity are available,
the magnitude of the estimate of the sample standard deviation, ![]() ,
depends on the
number of measurements, and consequently the calculated confidence
interval also depend on that number. For
,
depends on the
number of measurements, and consequently the calculated confidence
interval also depend on that number. For ![]() measurements, the confidence
interval of a single measurement can be expressed as
measurements, the confidence
interval of a single measurement can be expressed as ![]() . The
value of the parameter
. The
value of the parameter ![]() depends on the number of measurements. These
values can be read off of a table or explicitly calculated.1
depends on the number of measurements. These
values can be read off of a table or explicitly calculated.1
Assume that one has the following set of data shown in Table 1.
The sample standard deviation is given by (Eqn. 2).
Using Eqn 2, the data from Table 1, and the results from Eqn. 1, one computes the sample standard deviation as follows.
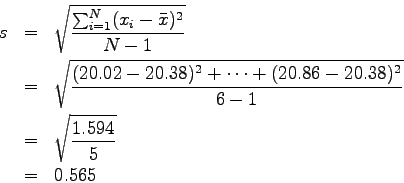
The 95% confidence interval would then be calculated by first looking
up (or calculating) the ![]() value for a confidence interval of 95%
and 5 degrees of freedom (that's N-1). The correct value, to 4 significant
figures, is 2.015. The correct way to list the measured value at
a 95% confidence interval is to write it with its proper confidence
limits using the number of significant digits in the measured quantity
as to determine the precision of the confidence interval. For example
value for a confidence interval of 95%
and 5 degrees of freedom (that's N-1). The correct value, to 4 significant
figures, is 2.015. The correct way to list the measured value at
a 95% confidence interval is to write it with its proper confidence
limits using the number of significant digits in the measured quantity
as to determine the precision of the confidence interval. For example
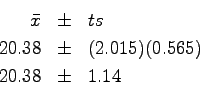
The 20.38 ![]() 1.14 is the experimental value with its 95% confidence
limit explicitly represented.
1.14 is the experimental value with its 95% confidence
limit explicitly represented.
Another less commonly used practice is to let the confidence interval actually determine the digits of precision represented in the final result. While this technique is more widely accepted using standard deviations, it can be done with confidence intervals as well. When large sets of data are collected, one can round the standard deviation to one significant figure and use the magnitude of the standard deviation to determine the number of significant figures for the final result.2 By analogy, if one has a smaller sample size ( where t-test statistics are more applicable ) one can use the confidence interval to determine the number of digits of precision to represent in the final result. In the example below, the confidence interval is rounded to one digit and that is used as a means to both round the average and also determine the number of significant digits to which it can be represented.
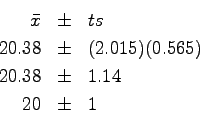
So in this example, the final result would only have two significant digits.
While you will not be expected to explicitly calculate ![]() value,3
some might find the
method by which they are calculated interesting.
The
value,3
some might find the
method by which they are calculated interesting.
The ![]() value for a given confidence interval,
value for a given confidence interval, ![]() , and the
numbers of degrees of freedom,
, and the
numbers of degrees of freedom, ![]() , must satisfy
the following equation.
, must satisfy
the following equation.
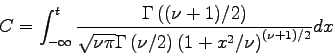 |
(3) |
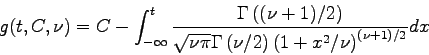 |
(4) |
This document was generated using the LaTeX2HTML translator Version 2002-2-1 (1.71)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 -local_icons -no_navigation ttest.tex
The translation was initiated by Andrew J. Pounds on 2009-05-25